Getting an intuition about splitting secrets
To understand how we might split a secret, let’s look at the standard 4 digit combination lock as an example.

Splitting a secret badly
In a 4 combination lock, there is a total of 10,000 combinations. If we were to simply split it into four parts and store them physically, then each part found would drastically reduce the difficulty of unlocking the lock.
Imagine a code: 7296, if the numbers 7, 2, and 9 were discovered, then the code could be found in 10 attempts, although, if the order of digits were unknown, it could take up to 1190 attempts.
This is the equivalent of splitting your seed words into chunks; it just isn’t a great idea.
Splitting a secret correctly
A quick debrief: the % symbol is a mathematical operator known as modulo, and it calculates the remainder after division. For example, 201 % 100 would equal 1 because 201 is divisible by 100 twice, leaving a remainder of 1 (simplified: 201/100 = 2 remainder 1, so 201 % 100 = 1).
Imagine, that instead, we split the code into four parts that can be combined with the following formula:
(a + b + c + d) % 9999
The four parts could be 1234, 3833, 8929, and 3299; (1234 + 3833 + 8929 + 3299) % 9999 = 7296 (do the math, use a calculator or even ask the internet if you want).
Revealing even three of these parts would reveal nothing about the fourth code, nor the final code.
Every part is 4 digits long, making each one just as difficult to discover as the other and most importantly, each part is just as difficult to guess as the final code itself, even if multiple parts are already discovered.
A nice visual aid to understanding the modulo operator is the number wheel. Imagine a number wheel from 0 to 99, it would look like this:
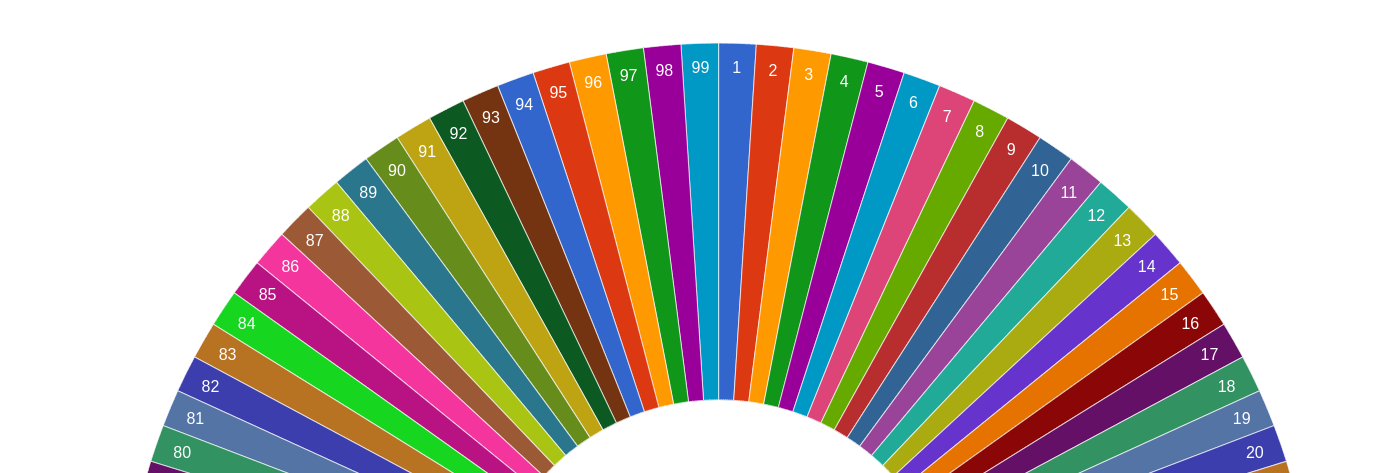
When adding two numbers, you would count on the wheel so that 80 + 55 would take you from 80 up to 99, and then continue through 0 all the way to 35.
Given any number between 0 and 99, what could the next possible number be? – Every single digit in the wheel is a possible answer which means that no matter how many parts of the formula a + b + c + d % 99 = answer you have, you are no closer to finding the final answer until you have all of the parts.
Pretty neat!
Splitting Bitcoin secrets
The above example was designed to give an intuition as to how a secret could be split into multiple, similarly difficult to guess parts, in a way such that no part gives any clue about the other parts.
A convenient mathematical operation that can be used efficiently by computers on large numbers is the XOR operator. In fact, the operation can be much easier for us to do by hand than a modulous operation with large numbers too.
With XOR, we can take any large number and merge it with many others to get a product. The order of operation is not important, so the parts can be later combined in any order, which allows us to avoid attaching hints such as “1 of 3” to our backups which would give away exactly how many parts to look for.